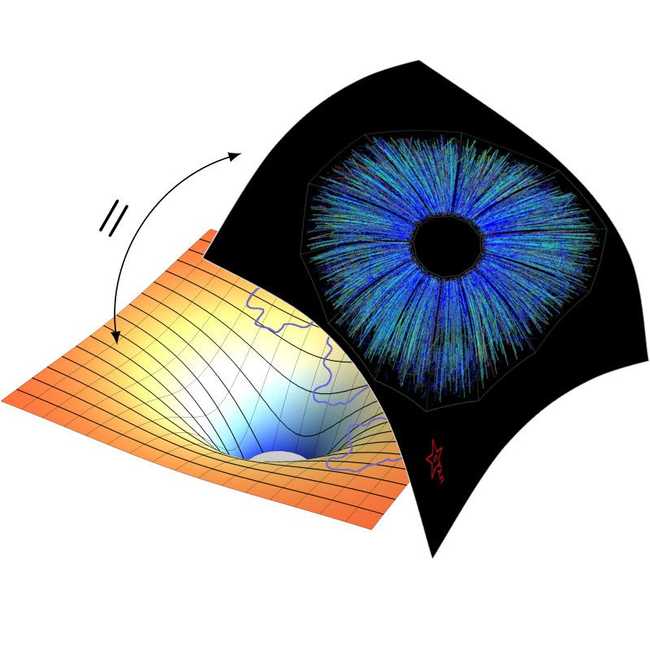In this course, we will explore the holographic principle, stating that a volume of space can be equivalently described by its lower-dimensional boundary. One might think of a hologram which captures a three-dimensional object on a two-dimensional surface. A particular well studied realization of this idea is the AdS/CFT correspondence which conjectures the equivalence between quantum gravity in Anti-de Sitter (AdS) space and a conformal field theory (CFT) on its boundary. This conjecture is very hard to prove because when one of the two theories is weakly coupled, allowing to use perturbation theory to study it, the other one is strongly coupled - making it very hard to analyse. Despite still being a conjecture, this idea had a huge impact on high-energy physics with an extremely broad range of applications. Latter range from new insights into strongly coupled quantum field theory, required for example to study extreme states of matter like quark-gluon-plasmas or superconductors, to the analysis of black-hole evaporation, that ultimately requires a handle on quantum gravity. We take this as a motivation to study this duality and its main actors in this course in detail. The lectures are tailored towards master and PhD students who are at least familiar with

• electrodynamics
• special relativity
• quantum mechanics.

Basic knowledge of general relativity and quantum field theory is definitely an advantage, but we review their most salient aspects in case you have not yet attended a specialized course on them yet. We will mostly follow the book

• Martin Ammon, Johanna Erdmenger: Gauge/Gravity Duality,

but you might also want to have a look at

• Lewis Ryder: Introduction to General Relativity
• Michael Peskin, Daniel Schroeder: Quantum Field Theory
• Barton Zwiebach: String Theory

for more details on the main actors of the gauge gravity duality.

We will have 2 hours of lectures and 2 hours of tutorial each week. Exercises will be posted here a week before the tutorial they are discussed in. Please keep in mind that active participation in the tutorials is important to pass the course. M.Sc. Luca Scala will be the assistant for the tutorials. Please fell free to contact him or me if you have any questions.

Important: Students will be assigned to exercise problems by the system described here, before the tutorial. Please familiarise yourself with this system and do not forget to indicate your preferences.

Exam: We decided to have an oral exam (not longer than 45 minutes) for this course in the afternoon of Tuesday, the 11th of February 2025. The exact time will be individually assigned. To help you prepare, here is a preliminary list of relevant topics:

1. Anti-de Sitter space
   • isometries, and the corresponding isometry group
   • construction as hypersurface embeed into $\mathbb{R}^{d,2}$
   • bounday and its properties
   • different coordinate systems
2. Large N limit of SU(N) (super) Yang-Mills theory
   • planar diagrams
   • relation of the partition function to the string partition function
3. Conformal symmetry and supersymmetry
   • Coleman-Mandula theorem
   • algebras
   • representations
   • resulting simplifications in QFT calcuations
   • anomalies
4. String theory basics
   • specturm of open and closed strings
   • string perturbation theory
   • super strings and GSO projection
   • D-branes from the world-volume perspective (DBI action) and from the target-space perspective (black black solution)
5. AdS CFT correspondence
   • near horizon limit for a stack of N D3 branes
   • ...

Retake Exam: If required, the retake exam can be taken on the afternoon of Tuesday, the 18th of February 2025. The same conditions as for the exam apply.

Additional material for the individual lectures, including the exercises which we discuss in the tutorials, will appear here in due time.