An Introduction to String Theory
USOS
One of the greatest puzzles in theoretical physics is to find a consistent quantum theory of gravity, the only one of the four fundamental forces we do not know how to quantise yet. Although decades of intensive work, we have no conclusive answer to this problem. Currently one of the main contender in race towards quantum gravity is String Theory. It is based on a simple but far reaching idea, to substitute point-like particles with extended objects, strings and membranes. In this course, we will explore the implications of this idea. More precisely, we study the bosonic string and see that it not onl describes gravity but also gauge theories on D-branes. Gauge theories are required to describe the remainig three fundamental forces. This renders string theory to a theory of everything. The course is tailored towards master and PhD students who are familiar with
- electrodynamics
- special relativity
- quantum field theory.
Basic knowledge of general relativity is an advantage, but you also should be find if you did not have attended the GR course yet. There are many good books on the subject, four that I like are
- Barton Zwiebach: A First Course in String
- Blumenhagen, Lüst, Theisen: Basic Concepts of String Theory
- Polchinski: String Theory, Volume 1
- Johnson: D-Branes
Moreover, David Tong has some excellent lecture notes. We will have 2.5 hours of lectures and 2.5 hours of tutorial each week. Exercises will be posted here a week before the tutorial they are discussed in. Please keep in mind that active participation in the tutorials is important to pass the course. M.Sc. Luca Scala will be the assistant for the tutorials. Please fell free to contact him or me if you have any questions.
There are many other interesting approaches to Quantum Gravity and string theory is by far not the only one. There is another course this semester, Introduction to Quantum Gravity, which I highly recommend.
Important: Students will be assigned to exercise problems by the system described below, before the tutorial. Please familiarise yourself with this system and do not forget to indicate your preferences.
Additional material for the individual lectures, including the exercises which we discuss in the tutorials, will appear here in due time.
- Why, what and how - from the relativistic particle to the Nambu-Goto actionTutorial13.03.2023 23:00, exercise
Please note that there are no exercise assignments for the first tutorial. However, we will use a few mintues to explain how exercise problems are assigned. To prepare, it would be great if you could already follow the instructions outlined in the pdf you find under the exercise link above. For the remainder of the tutorial, we continue with the lecture. This gives us time to motivate why we need string theory, to look at the relativistic point particle and to show how it can be generalised to the string.
Note: There were some questions today in the lecture about the history of String Theory. A nice account of this topic is given by the short article arXiv:1201.0981 of John Schwarz, one of the founders of the field.
- Classical string and the Polyakov action
- Symmetries of the classical string, especially, Weyl invariance
- Mode expansion and open/closed string boundary conditions
- Old covariant quantisation, Virasoro algebra and physical states
- Physical spectrum, massless states, no-ghosts theorem, critical dimension
- Light-cone quantisation (tutorial) and modern covaraint quantisation in the BRST formalism with bc-ghost system (lecture)
- Conformal field theory (CFT) and operator product expansion (OPE) in a nutshell
On CFT, one could and should give a full semester course. We cannot do this here, but I try to give you a self-contained introduction. CFT is crucial to discuss interactions between strings. Therefore, we have to gain a basic understanding of it.
- Vertex operators and a first glance at string perturbation theory
Reading: [BLT] section 6.1 and 6.2
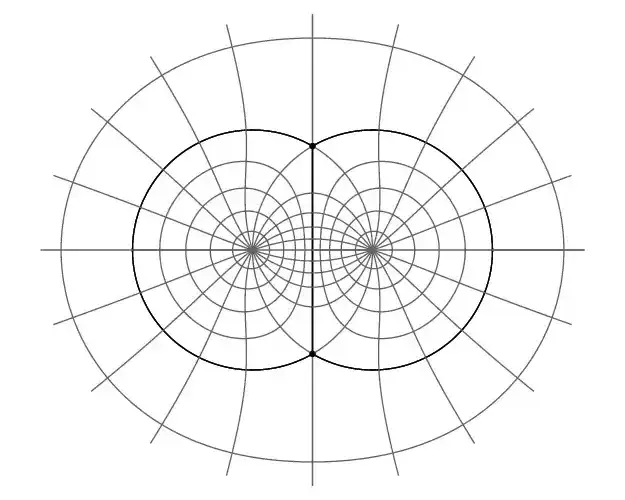
String perturabation theory is very beautiful. It crucially depends on the moduli space of Riemann surfaces. Unfortunately, we do not have enough to look at this topic in more detail. For those of you how are interested, section 6.2 of the book by Blumenhagen, Lüst and Theisen is a very good starting point. To make you a bit more curious, here is a picutre of a tree-point vertex in the complex plane.
Much more details how it arises can be found in section 4.2 of my PhD thesis [H36].
- Low energy effective actions and compactifications
- Closed strings on circles and T-dualtiy
- D-branes and gauge theories