Hi, I am Falk Hassler, an assistant professor at the Institute of Theoretical Physics at the University of Wrocław.

Before coming here in 2021, my life as a postdoc started in 2015, when I finished my PhD at the Ludwig Maximilian University of Munich. Since then, it has not been short of adventures. I had the opportunity to work in many exciting places with great people from all over the world: New York City, Chapel Hill (North Carolina), Philadelphia, Oviedo (Spain) and College Station (Texas) have been home to my family (wife Antje and our daughter Amy who was born in Philly) and me. After growing up in a small town in the northeast of Germany, I would have never dreamed that physics would lead me to all these incredible places one day. You can find more details in my CV.

Research

Lay version

Imagine we take a coffee mug and zoom in with a very powerful microscope. Eventually, we will discover that it is made out of atoms. These atoms have protons and neutrons in their core which consists of quarks held together by gluons. We don't have machines yet to zoom in much further. But one thing is certain: something dramatic has to happen at the incredibly small scale of $10^{-35}$ meters. At this point, the two fundamental ingredients of physics, general relativity and quantum field theory, start to contradict each other.

My research takes us exactly to this point. Although we do not have any experimental data at this scale yet, the last 50 years have produced some incredible ideas of what we might find. All of them are based on the fundamental mechanisms in physics that we already have confirmed experimentally. The most studied idea is that extended objects, strings, should ultimately substitute point particles.

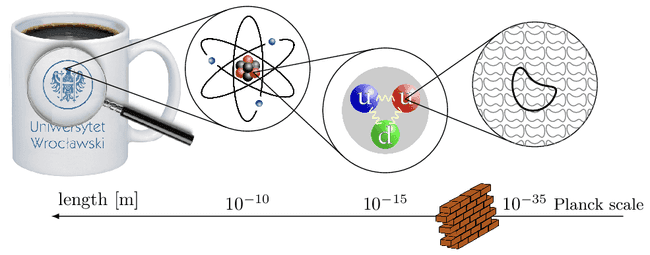
Strings are so fundamental that not only particles are made of them but also the interactions between them and even spacetime itself.

Hence, we face a crucial change of paradigms. Point particles have a natural notion of distance. Take as a simple a free particle on a ring. Its energy spectrum is indirectly proportional to the radius. Thus, we could easily distinguish between large and small rings. Distance between points is also the defining concept in Riemannian geometry that underpins general relativity.

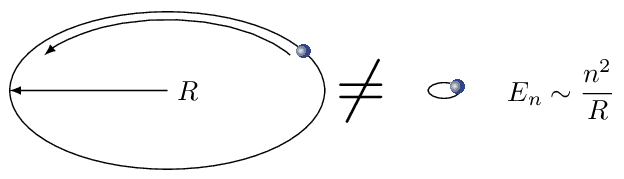
Things become more subtle if we look at strings because, in addition to the centre of mass motion of point particles, they can wind around the circle. Hence, their spectrum is characterised by two quantum numbers. Remarkably, it is the same on two circles, one larger and the other one smaller than the length of the string. Just the role of momentum and winding gets flipped. This effect is called T-duality, and it obfuscates the clear notion of distance neeed to define geometry. Therefore strings require ultimately to work with a generalisation of geometry.

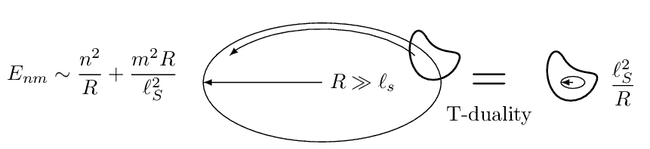
My work has revealed how this adapted version of geometry can capture T-dualities far beyond the simple example we have just discussed. In contrast to a circle or a torus, the spacetimes I am interested in are curved.

Strings in curved backgrounds automatically induce higher curvature corrections that modify the Einstein-Hilbert action of point particles. These corrections are essential to understanding how a quantum theory of gravity might resolve singularities at the centre of black holes or the Big Bang. Thus, my current efforts focus on how T-duality allows to explicitly compute these corrections. Moreover, my work gives a new handle on integrable string models, which are an indispensable tool in the long-standing quest of proving the AdS/CFT correspondence, perhaps the successful spin-offs of string theory.

For experts

Using dualities in string theory, I explore quantum field theory and quantum gravity at strong coupling, very high energies and small distances. Important ingredients in my work are double/exceptional field theory, an effective target space description of string/M-theory, which makes T-/U-dualities manifest, and (super)conformal field theories, (S)CFTs, in two and more dimensions. On the formal side, I look into the underlying principles of generalised geometry, non-commutative or even non-associative geometry and, especially, how they naturally arise from strings and higher dimensional membranes probing spacetime. String field theory and worldsheet renormalisation group flow, which allow extracting new mathematical structures from the $\sigma$-model that underlies the string's dynamics, are powerful tools I rely on. Although this is still a perturbative approach, it can point out underlying symmetry principles that allow accessing the non-perturbative regime.

A prominent example is supersymmetry. It allows studying certain protected sectors of a theory (like BPS solutions) at strong coupling. These by the symmetry distinguished sectors are also indispensable for approaching higher-dimensional SCFTs, which usually do not have a weak coupling limit. Besides having all these fundamental aspects in mind, I am interested in applications. They range from flux compactifications over consistent truncations to simple toy models for inflation in cosmology. In the last years, I revealed an elementary link between Poisson-Lie T-duality and generalised geometry. It brings together two thriving research communities and paves the way for important discoveries. Among them is a new approach to one of the biggest questions in contemporary physics: What is the fundamental structure of space and time? I am exploring this and related questions together with my research team.

Contact

Address:

Institute of Theoretical Physics

University of Wrocław

pl. M. Borna 9

50-204 Wrocław, Poland

Office:

448

E-Mail:

Skype:

falkhassler

Phone:

+48 71 375-9241

Mobile:

+48 573 551 052